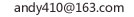y=arccotx的图象是一个在实数域R上单调递减的函数图像,不具有周期性和常见的奇偶性特征。以下是关于y=arccotx图象的详细描述:
单调递减:
- y=arccotx在实数域R上是单调递减的,这意味着随着x的增大,y的值会逐渐减小。
非周期性:
- 与正切函数不同,反余切函数y=arccotx不具备周期性。因此,其图象上不会出现重复的模式或周期性波动。
非奇非偶性:
- y=arccotx既不是奇函数也不是偶函数。这意味着在图象上,既找不到关于y轴的对称性,也找不到关于原点的对称性。
图象形态:
- 从图象上看,y=arccotx的图象类似于一个逐渐下降的曲线,随着x的增大,y值逐渐趋近于0,而当x趋近于负无穷或正无穷时,y值分别趋近于π/2和π/2。
与余切函数的关系:
- y=arccotx是余切函数y=cotx在区间的反函数。因此,y=arccotx的图象与y=cotx的图象在区间内存在反函数关系。
综上所述,y=arccotx的图象是一个单调递减、非周期、非奇非偶的函数图像,具有独特的形态和性质。
温馨提示:答案为网友推荐,仅供参考
y=arccotx的图象是什么样的啊,急急急!!!
y=arccotx,是反余切函数,反余切函数是单调递减函数。其图形如下图所示:反余切函数的定义域为:反余切函数的值域:
y=arccotx的图象是什么样的啊,急急急!!!
从图象上看,y=arccotx的图象类似于一个逐渐下降的曲线,随着x的增大,y值逐渐趋近于0,而当x趋近于负无穷或正无穷时,y值分别趋近于π\/2和π\/2。与余切函数的关系:y=arccotx是余切函数y=cotx在区间的反函数。因此,y=arccotx的图象与y=cotx的图象在区间内存在反函数关系。综上所述,y=arccot...
y=arccotx的图象是什么样的啊,急急急!!!
当我们谈论y=arccotx的图象时,它实际上是余切函数y=cotx在区间(0,π)的反函数的图形。这个反函数在实数域R上的性质独特,它是一个单调递减的函数。不同于正切函数的周期性,反余切函数不具备周期性,它的图象没有重复的模式。同时,它并不具备常见的奇偶性特征,即它既不是奇函数也不是偶函数,...
函数y=arccotx是啥
其图象是:反余切函数y=arccotx在定义域R内是减函数。反余切函数y=arccotx既不是奇函数,也不是偶函数。
y=arc cot x的函数图像是?
见图。蓝线为y=arc cot x的图像。为对比起见,y = cot(x)的图像(红线)也一并画出。
arc cotx表示什么?
解题过程如下:arcctot x是反余切函数,是余切函数y=cotx(x∈[0,π])的反函数。它的函数图形如下,由图形可以看出当x趋近正无穷时函数值为0,趋近负无穷时函数值为π。
反三角余切函数的图象 数学达人帮我画一下!!! 我不清楚它的性质!
函数名称 反余切函数 解析式 y=arccotx 图象 :反余切曲线(如图)性质:1.定义域 R 2.值域 (0, π)3.有界性 0<y<π 4.最值 无 5.单调性 减函数 6.奇偶性 奇函数 7.周期性 无 8.对称性 对称中心(0, π\/2)9.渐近线 ...
y=arc cot x的函数图像是?
见图。蓝线代表了函数y=arccotx的图像,它描绘了反余切函数的特性。为了更好地理解其性质,同时也画出了y=cot(x)的图像(红线)。通过这两条曲线的对比,我们可以更直观地观察到,反余切函数图像在x轴上呈现出独特的波动形态。反余切函数y=arccotx是一个重要的数学函数,它的图像展示了一个有趣的...
反三角函数的图像是什么样子的
x=tan y在(-π\/2,π\/2)上的反函数,叫做反正切函数。记作arctanx,表示一个正切值为x的角,该角的范围在(-π\/2,π\/2)区间内。定义域R,值域(-π\/2,π\/2)。4、反余切函数 x=cot y在(0,π)上的反函数,叫做反余切函数。记作arccotx,表示一个余切值为x的角,该角的范围...
y=arccotx的函数图像是?
y=arccotx的图像呈现出双曲线的特征。这是因为反余切函数具有渐近线和对称性等典型特征。这种函数的图像大致是一个开放的双曲线形状,其中的一部分。其渐近线一般垂直于x轴,反映了函数值的极限状态。三、图像的具体形态 具体来说,当x趋向于正无穷或负无穷时,y值逐渐接近一定的角度值,这表明函数的值域...
y=arccotx,是反余切函数,反余切函数是单调递减函数。其图形如下图所示:反余切函数的定义域为:反余切函数的值域:
y=arccotx的图象是什么样的啊,急急急!!!
从图象上看,y=arccotx的图象类似于一个逐渐下降的曲线,随着x的增大,y值逐渐趋近于0,而当x趋近于负无穷或正无穷时,y值分别趋近于π\/2和π\/2。与余切函数的关系:y=arccotx是余切函数y=cotx在区间的反函数。因此,y=arccotx的图象与y=cotx的图象在区间内存在反函数关系。综上所述,y=arccot...
y=arccotx的图象是什么样的啊,急急急!!!
当我们谈论y=arccotx的图象时,它实际上是余切函数y=cotx在区间(0,π)的反函数的图形。这个反函数在实数域R上的性质独特,它是一个单调递减的函数。不同于正切函数的周期性,反余切函数不具备周期性,它的图象没有重复的模式。同时,它并不具备常见的奇偶性特征,即它既不是奇函数也不是偶函数,...
函数y=arccotx是啥
其图象是:反余切函数y=arccotx在定义域R内是减函数。反余切函数y=arccotx既不是奇函数,也不是偶函数。
y=arc cot x的函数图像是?
见图。蓝线为y=arc cot x的图像。为对比起见,y = cot(x)的图像(红线)也一并画出。
arc cotx表示什么?
解题过程如下:arcctot x是反余切函数,是余切函数y=cotx(x∈[0,π])的反函数。它的函数图形如下,由图形可以看出当x趋近正无穷时函数值为0,趋近负无穷时函数值为π。
反三角余切函数的图象 数学达人帮我画一下!!! 我不清楚它的性质!
函数名称 反余切函数 解析式 y=arccotx 图象 :反余切曲线(如图)性质:1.定义域 R 2.值域 (0, π)3.有界性 0<y<π 4.最值 无 5.单调性 减函数 6.奇偶性 奇函数 7.周期性 无 8.对称性 对称中心(0, π\/2)9.渐近线 ...
y=arc cot x的函数图像是?
见图。蓝线代表了函数y=arccotx的图像,它描绘了反余切函数的特性。为了更好地理解其性质,同时也画出了y=cot(x)的图像(红线)。通过这两条曲线的对比,我们可以更直观地观察到,反余切函数图像在x轴上呈现出独特的波动形态。反余切函数y=arccotx是一个重要的数学函数,它的图像展示了一个有趣的...
反三角函数的图像是什么样子的
x=tan y在(-π\/2,π\/2)上的反函数,叫做反正切函数。记作arctanx,表示一个正切值为x的角,该角的范围在(-π\/2,π\/2)区间内。定义域R,值域(-π\/2,π\/2)。4、反余切函数 x=cot y在(0,π)上的反函数,叫做反余切函数。记作arccotx,表示一个余切值为x的角,该角的范围...
y=arccotx的函数图像是?
y=arccotx的图像呈现出双曲线的特征。这是因为反余切函数具有渐近线和对称性等典型特征。这种函数的图像大致是一个开放的双曲线形状,其中的一部分。其渐近线一般垂直于x轴,反映了函数值的极限状态。三、图像的具体形态 具体来说,当x趋向于正无穷或负无穷时,y值逐渐接近一定的角度值,这表明函数的值域...
相似回答
大家正在搜