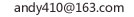这个是属于定积分。定积分在图像上就表示一条曲线与X轴围城的面积。
解
①由∫x^adx=1/(1+a)*x^(1+a)+C可知
∫x^(1/2)dx=∫√xdx=1/[1+(1/2))]*x^[1+(1/2))]
=2/3*x^(2/3)+C
∫x^2=1/3*x^3+C
②∫【a,b】f(x)dx=F(x)|【a,b】=F(b)-F(a),
其中F(x)为f(x)的原函数
③∫【a,b】[f(x)-g(x)]dx={F(b)-G(b)}-{F(a)-G(a)}
因此
∫【0,1】{√x-x^2}dx=[2/3*x^(2/3)-1/3*x^3]|【0,1】
=(2/3-1/3)-(0-0)
=1/3
不定积分的公式
1、∫ a dx = ax + C,a和C都是常数
2、∫ x^a dx = [x^(a + 1)]/(a + 1) + C,其中a为常数且 a ≠ -1
3、∫ 1/x dx = ln|x| + C
4、∫ a^x dx = (1/lna)a^x + C,其中a > 0 且 a ≠ 1
5、∫ e^x dx = e^x + C
6、∫ cosx dx = sinx + C
7、∫ sinx dx = - cosx + C
8、∫ cotx dx = ln|sinx| + C = - ln|cscx| + C
温馨提示:答案为网友推荐,仅供参考
第1个回答 推荐于2017-10-01
两曲线和x轴围成了两个曲边三角形,蓝色面积(图中用A表示)等于大的面积减去小的∫X^½·dx-∫X^2·dx=∫(x^½-x^2)·dx
积分原理具体百度。所谓面积元素(dA)就类似你图里蓝色部分中的分割出的紫色矩形,每个矩形宽都足够小,为dx,对应的长(比如宽的左端点是x。)为(x。^½-x。^2);把所有紫色矩形面积(面积元素)加起来近似等于蓝色部分面积。
最后一步是牛顿莱布尼兹公式(导函数两点间的积分值等于原函数两点值的差)。本回答被网友采纳
积分原理具体百度。所谓面积元素(dA)就类似你图里蓝色部分中的分割出的紫色矩形,每个矩形宽都足够小,为dx,对应的长(比如宽的左端点是x。)为(x。^½-x。^2);把所有紫色矩形面积(面积元素)加起来近似等于蓝色部分面积。
最后一步是牛顿莱布尼兹公式(导函数两点间的积分值等于原函数两点值的差)。本回答被网友采纳
第2个回答 推荐于2018-02-28
这个是属于定积分。定积分在图像上就表示一条曲线与X轴围城的面积。。
这个图的两条曲线一个是Y=根号X 一个是Y=X2.
阴影部分的面积就是第一个的面积减去第二个的面积。。
所以你看到的面积元素也就是这么来的。。
我这么说你明白了么?追问
这个图的两条曲线一个是Y=根号X 一个是Y=X2.
阴影部分的面积就是第一个的面积减去第二个的面积。。
所以你看到的面积元素也就是这么来的。。
我这么说你明白了么?追问
最后哪一步A等于、等于、等于,都是怎么算出来的,能详细的讲一下么?用的什么公式啊?
本回答被提问者和网友采纳第3个回答 2017-08-27
解
①由∫x^adx=1/(1+a)*x^(1+a)+C可知
∫x^(1/2)dx=∫√xdx=1/[1+(1/2))]*x^[1+(1/2))]
=2/3*x^(2/3)+C
∫x^2=1/3*x^3+C
②∫【a,b】f(x)dx=F(x)|【a,b】=F(b)-F(a),
其中F(x)为f(x)的原函数
③∫【a,b】[f(x)-g(x)]dx={F(b)-G(b)}-{F(a)-G(a)}
因此
∫【0,1】{√x-x^2}dx=[2/3*x^(2/3)-1/3*x^3]|【0,1】
=(2/3-1/3)-(0-0)
=1/3
不懂可以追问
①由∫x^adx=1/(1+a)*x^(1+a)+C可知
∫x^(1/2)dx=∫√xdx=1/[1+(1/2))]*x^[1+(1/2))]
=2/3*x^(2/3)+C
∫x^2=1/3*x^3+C
②∫【a,b】f(x)dx=F(x)|【a,b】=F(b)-F(a),
其中F(x)为f(x)的原函数
③∫【a,b】[f(x)-g(x)]dx={F(b)-G(b)}-{F(a)-G(a)}
因此
∫【0,1】{√x-x^2}dx=[2/3*x^(2/3)-1/3*x^3]|【0,1】
=(2/3-1/3)-(0-0)
=1/3
不懂可以追问
第4个回答 2017-09-04
x轴任意划分,并且在每一个小分段中的取值也是任意的,而∑f(ξi)△xi当max△xi→0时,的极限总存在,才能叫定积分。 所以只要定积分存在,△x是任意的。只是书上为了方便,划为了等分。
如何用微积分求出任意图形的面积?我看到网上很多看到不会算的面积题就...
1. 当图形可以用函数 f(x) = y 表示时,我们可以通过积分来求解其面积。2. 如果图形由多个部分组成,可能需要使用分段函数来描述。3. 举例来说,如果有两个函数 f(x) 和 g(x),它们分别描述了两条曲线,且 f(x) 在 g(x) 上方,我们想要计算区间 [a, b] 上的闭区间面积。4. 该面积...
怎么用微积分算面积?举个例子
1. 首先,我们需要找到 \\( f(x) = \\sqrt{x} \\) 的一个原函数。原函数是导数的逆运算,因此我们对 \\( f(x) \\) 进行积分。对于 \\( f(x) = \\sqrt{x} \\),其原函数是 \\( F(x) = \\frac{2}{3}x^{\\frac{3}{2}} \\)。2. 接下来,我们使用定积分的公式来计算面积:\\[\\int...
如何计算曲线围成的面积?用微积分,举例说明,附过程。
1. 首先,确定曲线的方程为 y = f(x)。2. 然后,确定 x 的取值范围为 [a, b]。3. 接下来,计算曲线与 x 轴的垂线以及 x 轴围成的面积,公式为:S = ∫(从 a 到 b) f(x) dx。4. 在此公式中,(a, b) 表示定积分的上限和下限。
如何用微积分求出任意图形的面积?我看到网上很多看到不会算的面积题就...
3. 计算两个函数曲线之间的面积的通式为:s=∫(a,b)[f(x)-g(x)]dx,这里 a 和 b 是指定区间上的两个点,x 值的变化范围。4. 通过应用微积分的基本定理,我们可以找到这个积分,从而得到所求图形的面积。5. 需要注意的是,对于更复杂的图形,可能需要使用多个定积分来求得总面积,这可能涉...
如何用微积分求面积?
• 若区域由多条曲线围成,需分别计算各部分面积再相减。实例 假设你想求由 (y=x^2) 和 (y=2-x) 在第一象限围成的区域面积。首先解方程组找出交点,然后确定积分上下限,最后计算定积分。以上是使用微积分求曲边图形面积的基本方法。实践中,根据具体函数和区域形状,可能需要应用不同的...
怎么用微积分算面积?举个例子
①由∫x^adx=1\/(1+a)*x^(1+a)+C可知 ∫x^(1\/2)dx=∫√xdx=1\/[1+(1\/2))]*x^[1+(1\/2))]=2\/3*x^(2\/3)+C ∫x^2=1\/3*x^3+C ②∫【a,b】f(x)dx=F(x)|【a,b】=F(b)-F(a),其中F(x)为f(x)的原函数 ③∫【a,b】[f(x)-g...
用微积分算面积,要详细步骤
先把两个方程联立起来解出(x1,y1)及(X2,y2)其中一个是(0,0).先从第二方程积分到x2再减去第一方程积分到x2.
如何用微积分求出任意图形的面积?我看到网上很多看到不会算的面积题就...
用微积分计算任意图形的面积,一般需要前提:这个任意的图形可以用函数来表示,并可以解析成y=f(x)形式。或者这个任意图形可以用分段函数来表示。举例说明,两个不同的函数y1=f(x),y2=g(x),都为曲线而非直线函数,且都在定义在x轴上方,y1在y2的上方,则计算区间[a,b]上的面积通式为:s=∫...
微积分在求面积和体积上,是怎么用的,举例说明
1. 微积分在求解几何问题时,尤其是面积和体积的计算,运用了无限分割和求和的概念。2. 以圆的面积为例,假设圆的半径为r,圆心位于原点,圆的方程为x^2 + y^2 = r^2。3. 对于第一象限和第二象限内的半圆,其边界可以表示为y = √(r^2 - x^2),与x轴交于点(-r, 0)和(r, 0)。
微积分求面积公式例子
∫x1\/2dx=∫√xdx=1\/[1+(1\/2)]·x[1+(1\/2)]=2\/3·x2\/3+C 同样地,当a为2时,我们得到:∫x2dx=1\/3·x3+C 进一步,对于区间[a,b]上的定积分,其计算公式为F(x)|ab=F(b)-F(a),其中F(x)是f(x)的原函数。以此公式为基础,我们能够计算特定区间内的函数差异。比如,要...
1. 当图形可以用函数 f(x) = y 表示时,我们可以通过积分来求解其面积。2. 如果图形由多个部分组成,可能需要使用分段函数来描述。3. 举例来说,如果有两个函数 f(x) 和 g(x),它们分别描述了两条曲线,且 f(x) 在 g(x) 上方,我们想要计算区间 [a, b] 上的闭区间面积。4. 该面积...
怎么用微积分算面积?举个例子
1. 首先,我们需要找到 \\( f(x) = \\sqrt{x} \\) 的一个原函数。原函数是导数的逆运算,因此我们对 \\( f(x) \\) 进行积分。对于 \\( f(x) = \\sqrt{x} \\),其原函数是 \\( F(x) = \\frac{2}{3}x^{\\frac{3}{2}} \\)。2. 接下来,我们使用定积分的公式来计算面积:\\[\\int...
如何计算曲线围成的面积?用微积分,举例说明,附过程。
1. 首先,确定曲线的方程为 y = f(x)。2. 然后,确定 x 的取值范围为 [a, b]。3. 接下来,计算曲线与 x 轴的垂线以及 x 轴围成的面积,公式为:S = ∫(从 a 到 b) f(x) dx。4. 在此公式中,(a, b) 表示定积分的上限和下限。
如何用微积分求出任意图形的面积?我看到网上很多看到不会算的面积题就...
3. 计算两个函数曲线之间的面积的通式为:s=∫(a,b)[f(x)-g(x)]dx,这里 a 和 b 是指定区间上的两个点,x 值的变化范围。4. 通过应用微积分的基本定理,我们可以找到这个积分,从而得到所求图形的面积。5. 需要注意的是,对于更复杂的图形,可能需要使用多个定积分来求得总面积,这可能涉...
如何用微积分求面积?
• 若区域由多条曲线围成,需分别计算各部分面积再相减。实例 假设你想求由 (y=x^2) 和 (y=2-x) 在第一象限围成的区域面积。首先解方程组找出交点,然后确定积分上下限,最后计算定积分。以上是使用微积分求曲边图形面积的基本方法。实践中,根据具体函数和区域形状,可能需要应用不同的...
怎么用微积分算面积?举个例子
①由∫x^adx=1\/(1+a)*x^(1+a)+C可知 ∫x^(1\/2)dx=∫√xdx=1\/[1+(1\/2))]*x^[1+(1\/2))]=2\/3*x^(2\/3)+C ∫x^2=1\/3*x^3+C ②∫【a,b】f(x)dx=F(x)|【a,b】=F(b)-F(a),其中F(x)为f(x)的原函数 ③∫【a,b】[f(x)-g...
用微积分算面积,要详细步骤
先把两个方程联立起来解出(x1,y1)及(X2,y2)其中一个是(0,0).先从第二方程积分到x2再减去第一方程积分到x2.
如何用微积分求出任意图形的面积?我看到网上很多看到不会算的面积题就...
用微积分计算任意图形的面积,一般需要前提:这个任意的图形可以用函数来表示,并可以解析成y=f(x)形式。或者这个任意图形可以用分段函数来表示。举例说明,两个不同的函数y1=f(x),y2=g(x),都为曲线而非直线函数,且都在定义在x轴上方,y1在y2的上方,则计算区间[a,b]上的面积通式为:s=∫...
微积分在求面积和体积上,是怎么用的,举例说明
1. 微积分在求解几何问题时,尤其是面积和体积的计算,运用了无限分割和求和的概念。2. 以圆的面积为例,假设圆的半径为r,圆心位于原点,圆的方程为x^2 + y^2 = r^2。3. 对于第一象限和第二象限内的半圆,其边界可以表示为y = √(r^2 - x^2),与x轴交于点(-r, 0)和(r, 0)。
微积分求面积公式例子
∫x1\/2dx=∫√xdx=1\/[1+(1\/2)]·x[1+(1\/2)]=2\/3·x2\/3+C 同样地,当a为2时,我们得到:∫x2dx=1\/3·x3+C 进一步,对于区间[a,b]上的定积分,其计算公式为F(x)|ab=F(b)-F(a),其中F(x)是f(x)的原函数。以此公式为基础,我们能够计算特定区间内的函数差异。比如,要...
相似回答